Introdução
Aspectos associados às diferentes compreensões sobre como os modos do conhecimento se constituem são abordados pelo campo da Filosofia. Nesse sentido, encontram-se também várias preocupações referentes à formação humana e às formas como conhecimentos específicos podem se propagar, dentre os quais pode-se mencionar o conhecimento matemático.
A intenção de tematizar e problematizar peculiaridades e pretensões únicas da Matemática são contempladas pela Filosofia da Matemática. Questões envolvendo metodologia, epistemologia, ontologia, ou seja, reflexões que extrapolam os domínios da própria Matemática, são objetos pertinentes à Filosofia (SILVA, 2007).
Imre Lakatos, húngaro que nasceu em 1922, foi um importante filósofo do século XX, que teve seu olhar voltado tanto ao campo da ciência quanto da Matemática. O reconhecimento de seu trabalho está associado ao chamado “programa de pesquisa”, que é usado no intuito de explicar o desenvolvimento da ciência empírica. Em relação à Matemática, área a que se voltou principalmente no início de sua carreira, Lakatos embasou suas reflexões na história da Matemática, estendendo o fasificacionismo de Karl Popper aos enunciados da Matemática (MOLINA, 2001).
A proposta deste artigo é explorar possíveis relações entre algumas contribuições filosóficas de Lakatos, relacionadas ao método de provas e refutações, e aspectos relevantes à abordagem de problemas matemáticos no formato do Problem-Based Learning - PBL . Pretende-se explorar algumas ideias relativas à sua obra A Lógica do Descobrimento Matemático: Provas e Refutações (LAKATOS, 1978), fazendo considerações elementares acerca dos processos que envolvem a heurística.
Essa obra de Lakatos volta-se para o conhecimento matemático e suas contribuições geram possibilidades para que problemas matemáticos sejam resolvidos amparando-se em aspectos associados à lógica do descobrimento. A intenção é realizar algumas análises, que envolvam a resolução de um problema, considerando ideias advindas de princípios lakatosianos.
As reflexões deste artigo estruturam-se nas bases de uma pesquisa qualitativa, de cunho exploratório e bibliográfico. Sua composição se pauta na análise de referenciais teóricos, como: Cury (1994); Molina (2001); Silva e Moura (2015); Skovsmose (2007); Cardoso (1997), dentre outros, bem como a própria obra de Lakatos, Provas e Refutações, de 1978.
A partir das interpretações realizadas, busca-se relacionar algumas ideias com a resolução de problemas matemáticos que possam ser trabalhados na perspectiva do PBL. O propósito é de colocar os estudantes envolvidos como participantes efetivos das etapas de aprendizagem, como pode-se averiguar em procedimentos realizados por Lakatos, a intenção é explorar conhecimentos conceituais, atitudinais e procedimentais. A proximidade entre as abordagens realizadas por esse filósofo e o destrinchamento de discussões geradas com uma abordagem estimulada pelo PBL, podem encaminhar novas possibilidades de investigação, tanto no que concerne ao campo da Filosofia quanto da Matemática.
Características relevantes da obra
O pensamento que gerou as explanações deste estudo está ligado à produção de Lakatos chamada de A Lógica do Descobrimento Matemático: Provas e Refutações, de 1978. Essa obra demonstra uma oposição ao formalismo, que define Matemática como uma ciência amparada no trabalho com abstrações axiomáticas formais. O autor explora seus embasamentos filosóficos segundo alguns problemas da metodologia da Matemática, a qual tem como propósito abordar a lógica do descobrimento matemático.
Nesse sentido, Lakatos desafia o formalismo matemático, mas não se contrapõe diretamente a certas posições do dogmatismo matemático. Sua intenção é propiciar reflexões de que a Matemática não-formal, semiempírica, não pode progredir caso seja pautada no monótono aumento de teoremas e demonstrações, indubitavelmente estabelecidos (LAKATOS, 1978). Ou seja, o autor defende a ideia de que a Matemática é um campo de conhecimento falível, e, na interpretação de Skovsmose (2007, p. 2019), isso é “um ataque direto à ideologia da certeza”. Nessa visão, a Matemática é uma construção humana e, portanto, é passível de erros e dúvidas. Lakatos (1978, p. 18) afirma que é possível explorar a Matemática não-formal, embasando-se no “incessante aperfeiçoamento de opiniões por especulação e crítica, pela lógica das provas e refutações”.
À medida em que se avança na leitura de Provas e Refutações, compreende-se o quanto a lógica da certeza na Matemática é rejeitada por Lakatos. Vários processos de especulações e críticas, acerca de determinados conceitos matemáticos, são realizados no decorrer da obra e, conforme as ideias são desenvolvidas e/ou reconstruídas, o conhecimento no campo matemático também se aperfeiçoa. E, um dos princípios que está por trás desses processos refere-se ao método de provas e refutações.
Molina (2001), compreende que o método de provas e refutações de Lakatos é um método que alia, concomitantemente, a heurística Matemática e o entendimento da história dessa ciência. O autor destaca também a visão de que a concepção da Matemática é concebida diferentemente do empirismo lógico, estando sujeitas à crítica e revisão. Ou seja, ele:
tentou aplicar à Matemática a metodologia de conjecturas e refutações proposta por Popper para a ciência natural. Dessa forma, Lakatos deu um passo adiante de Popper, que ainda considerava a Matemática como formada por um conjunto de enunciados indubitáveis, verdadeiros de uma vez para sempre, e não sujeitos à refutação. Para Popper, como para os empiristas lógicos os enunciados matemáticos são verdades indubitáveis que não estão sujeitos a refutações (MOLINA, 2001, p.133).
Um novo olhar para o empirismo é dado por Lakatos, ao não considerar essas verdades eternas. Cury (1994), por exemplo, entende que as teorias quase-empíricas estão em oposição às teorias euclidianas, as quais se embasam em sistemas dedutivos (injetando o valor verdade por meio de demonstrações formais). Segundo a autora, os pressupostos quase-empiricistas, se desenvolvem de modo totalmente diferente dos formalistas, dentre os quais pode-se mencionar que: suas origens são amparadas em problemas, os quais têm suas soluções testadas, criticadas e refutadas; as propostas de soluções podem ser substituídas, não pelo acúmulo de conhecimento, mas mediante um refinamento das ideias, das críticas realizadas durante o processo de observação. E mais:
para Lakatos, o conhecimento matemático nasce da atividade humana, como parte de um processo social. Ele não considera a origem e a natureza dos entes matemáticos, mas o processo que transforma a criação privada em conhecimento público, processo esse que se desenvolve através de críticas e refutações. Para Lakatos, a busca da certeza absoluta é rejeitada, pois a Matemática é falível como qualquer outro conhecimento humano. A perspectiva heurística é adotada por ele como método de descoberta Matemática. Provar um teorema é um processo contínuo, que contínuo, que inicia com uma conjetura e parte para uma prova provisória, que será refutada por contraexemplos. Assim, a conjetura inicial vai sendo refinada (CURY, 1994, p.59).
Essa rejeição pela busca da certeza mostra que a heurística é um caminho para se promover diferentes descobertas Matemáticas, opondo-se aos ideais formalistas:
o formalismo desliga a história da Matemática da Filosofia da Matemática, uma vez que de acordo com o conceito formalista da Matemática, não há propriamente história da Matemática [...] O formalismo nega o status de Matemática à maioria do que comumente tem sido considerado Matemática e nada pode dizer sobre seu progresso. Nenhum dos períodos criativos e dificilmente qualquer dos períodos críticos das teorias Matemáticas seriam admitidos no céu formalista em que teorias Matemáticas habitam como o serafim, expurgado de todas as impurezas da incerteza terrestre. Contudo, os formalistas deixam, em geral, uma pequena porta traseira aberta para os anjos caídos (LAKATOS, 1978, p .14).
Essa colocação reforça a ideia do quanto o enfoque às teorias Matemáticas está atrelado aos sistemas formais, colocando de lado aspectos inerentes aos processos filosóficos que deram origem ao conhecimento matemático, negando fatores essenciais à própria Matemática. No entanto, essa “pequena porta traseira” deixada pelas abordagens formalistas, permite que novos olhares possam ser estabelecidos. Deste modo, a noção de empirismo foi reintroduzida, por Lakatos, na Filosofia da Matemática, e esse processo de provas e refutações faz referência a uma Matemática bem mais refinada em relação às observações empíricas trabalhadas em momentos anteriores (SKOVSMOSE, 2007). Segundo este autor, o falibilismo, proposto por Lakatos, é baseado na experiência sensória e, embora seja desenvolvido com um caráter puramente racional, podendo denotar uma perspectiva de mãos limpas sobre a Matemática, seria possível interpretar suas teorias sobre uma perspectiva radical, demonstrando um aspecto coletivo da construção Matemática, movimentada tanto pela Filosofia da Matemática quanto pela Educação Matemática.
Nesse sentido, pode-se explorar a resolução de problemas matemáticos contemplando-se algumas dessas ideias. Abordar problemas, explorando tanto conceitos matemáticos quanto suas potencialidades, aplicáveis a diferentes realidades, podem explorar vários aspectos heurísticos, que estão além do campo matemático. Isto é, normalmente, a Matemática é caracterizada como de mãos limpas e, para muitos, ela:
não está incluída na conexão, intrínseca ou não, entre desenvolvimento científico e desenvolvimento social, político, econômico e cultural [...] é um empreendimento intelectual puro, que se desenvolve de acordo com suas exigências lógicas e adquire seu significado particular (SKOVSMOSE, 2007, p.104).
A proposta de se trabalhar com problemas matemáticos busca relacionar aspectos inerentes a essa área e suas possíveis conexões com outras realidades, afinal, a Matemática não é uma ciência de mãos limpas. Assim como Lakatos destacou, esse campo de estudos não é fundamentado em verdades eternas, que não devem ser questionadas e refutadas. Por isso, entende-se que a abordagem de problemas por meio de perspectivas heurísticas, pode transpor aspectos amparados apenas no formalismo. O uso da Matemática não-formal, baseada em princípios quase-empíricos, se opõe a adoção de certezas absolutas, indubitáveis. A lógica de um descobrimento, seja ele matemático ou não, pode ocorrer a partir do uso e análise de problemas, e de suas possíveis soluções, as quais precisam ser testadas, criticadas e refutadas.
Os princípios lakatosianas que aqui são abordados visam denotar uma Matemática que transpõe aspectos formalistas, e que não se apresenta com uma ciência imparcial, sem relações com aspectos humanos, sociais e profissionais, por exemplo. Na próxima sessão, será realizada uma análise geral a respeito da obra Provas e Refutações e, em um momento posterior, são explanadas as etapas que giram em torno das características e do uso de um problema matemático, inspirados em um enfoque PBL, visando estabelecer algumas proximidades e/ou distanciamentos.
Provas e refutações - ampliando as reflexões
A obra A Lógica do Descobrimento Matemático - Provas e Refutações, de Lakatos baseia-se em sua tese doutoral e tem sido alvo de grande interesse por parte de educadores matemáticos. Sua estruturação apresenta dois capítulos que abordam a história de como a conjectura de Descartes-Euler se desenvolveu.
O primeiro capítulo contempla aspectos referentes a conjectura analisada, estabelecendo relações entre uma prova inicial e críticas (da prova e da análise da prova). Também são abordadas ideias a respeito: do uso de contraexemplos locais e globais; da formação de conceito; de discussões em torno de verdades Matemáticas; dentre outras considerações.
No segundo capítulo são realizadas outras discussões complementares sobre a conjectura. Consideram-se questões referentes a tradução da conjectura, outra prova e indagações acerca da finalidade da prova.
A obra Provas e Refutações também contém dois apêndices: um deles, explora um outro estudo de caso amparado no método de provas e refutações, considerando alguns aspectos como o princípio de continuidade e o conceito de convergência; o outro, aborda comparações entre os métodos dedutivista e heurístico, sendo este último apresenta-se como vantagem.
Em um contato inicial com sua obra pode-se notar que o autor critica aspectos ligados a abordagens formalistas e a falta de conexões entre a mesma e a História da Matemática. Isso se afirma logo nas primeiras páginas, quando Lakatos destaca que:
sob o atual domínio do formalismo, é se tentado a parafrasear Kant: a história da Matemática à falta da orientação da Filosofia, tornou-se cega, ao passo que a Filosofia da Matemática, voltando as costas aos fenômenos mais curiosos da história da Matemática, tornou-se vazia (LAKATOS, 1978, p.15).
Sendo assim, é proposto que o conhecimento matemático se desenvolva por meio do chamado Método de Provas e Refutações, compreendido como um método racional. Esse método admite:
a utilização de procedimentos incomuns a apresentações feitas em provas Matemáticas, logo a argumentação para a conclusão da veracidade da conjectura, admite a utilização de elementos não tão formais. Elementos que podem advir de outras áreas, não necessariamente de uma prévia lista de axiomas e postulados, ou teoremas anteriores como ocorre no método euclidiano dedutivo (TREVISAN, 2013, p.140).
Nessa obra, o trabalho com a construção racional da história da conjectura de Descartes-Euler para poliedros, na qual é válida a relação V - A + F = 2 (sendo que V representa o número de vértices, A, indica as arestas e F, o total de faces), se dá por meio de um diálogo que ocorre em uma sala de aula imaginária. Há vários alunos: Alfa, Beta, Gama, Ômega, Lambda, Pi, entre outros, e todos estabelecem discussões acerca de uma conjectura inicial e uma prova dada para a mesma, lançadas pelo professor da turma.
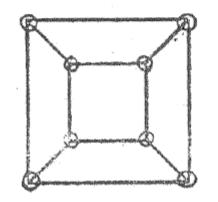
O início do diálogo é realizado pelo professor, que apresenta uma prova da conjectura, a partir da demonstração de Cauchy. Ele sugere que os alunos imaginem que o poliedro é oco e que, se removerem uma das faces, há como estender a superfície, ou seja, planificá-la. Mesmo que as faces e arestas fiquem deformadas, tanto os vértices como as arestas não irão se alterar, de forma que se, e apenas se, é válida a relação V - A + F = 2 para o poliedro original, V - A + F = 1 é válida para essa nova estrutura. Toma-se como exemplo a representação de um cubo, indicado pela Figura 1.
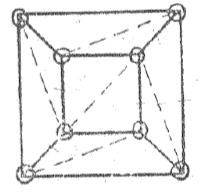
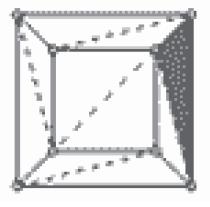
A segunda etapa amparou-se na triangularização desse poliedro, por meio do uso de diagonais. A medida que cada diagonal é desenhada, a relação V - A + F, não se altera. Isso poderá ser observado na Figura 2. Por fim, cada triângulo construído pode ser retirado um a um, removendo-se uma aresta, conforme a Figura 3a, ou duas arestas e um vértice, de acordo com a Figura 3b. Embora todo esse processo tenha seja feito, a conjectura inicial ainda se mantém. A ilustração a seguir representa essas etapas:
Etapas da triangulação do poliedro (cubo)
A partir da colocação do professor, um dos alunos, Alfa, questiona se realmente é possível estender a experiência feita com um cubo ou com um tetraedro, para qualquer poliedro. Também apresenta dúvidas em relação a validade de que os processos de planificação de um poliedro, também sejam verdade assim como ocorreu no caso do cubo. Um outro aluno, Beta, esboça dúvidas a respeito do segundo passo sugerido pelo professor e, um terceiro estudante, Gama, o questiona se há mesmo apenas duas alternativas no último passo. O interessante é que o professor diz que não há certeza, fato este que gera indagações sobre o que realmente é uma prova.
Cardoso (1997) descreve que os diálogos e análises realizadas entre o professor e os alunos geram contestações da prova em vários pontos. A prova inicial passa a ser reformulada e contraexemplos emergem ao longo do processo. Segundo a autora, esses contraexemplos são eliminados ou são convertidos em exemplos através das reformulações do conceito ou pelas correções feitas na prova usando a descoberta de lemas ocultos. Em meio a essas etapas, o conhecimento matemático cresce à medida que os aperfeiçoamentos são feitos e o campo matemático abordado vai sendo ampliado.
Nessa obra, não necessariamente, se segue uma ordem cronológica. Há o estabelecimento de uma ordem de desenvolvimento lógico que o autor acredita ser mais coerente. Silva e Moura (2015, p. 279) destacam que “no decorrer dos diálogos, Lakatos traz, nas notas de rodapé, a história genuína e documentada (em ordem não linear) da conjectura de Descartes-Euler, apresentando detalhes consideráveis”.
Cardoso (1997) observa que em Provas e Refutações há várias críticas em relação às metodologias do desenvolvimento do conhecimento, como o método de análise-síntese de Pappus, o indutivismo euleriano do século XVIII, o método euclidiano do século XIX e o formalismo do século XX. O método utilizado por Lakatos:
coloca em discussão questões muito delicadas como a verdade dos axiomas, o conteúdo empírico que eles podem conter, a prova, a certeza na Matemática. Sem dúvida, sua contribuição para a discussão filosófica na Matemática é imensa. Ele estendeu à Matemática a Filosofia falseacionista de Popper, abrindo portas para a constituição de uma Filosofia falibilista ou quase-empirista (como alguns querem) (CARDOSO, 1997, p.87).
Essas características relacionadas ao uso e interpretação de provas em Matemática foi bem discutida nos diálogos elaborados em Provas e Refutações. Em certo momento há a seguinte colocação:
Professor: Espero que agora todos vocês percebam que as provas, muito embora possam não comprovar, certamente ajudam a melhorar a conjectura. Os barradores de exceções melhoram-na muito, mas melhorar era independente de comprovar. No nosso método melhora comprovando. Essa unidade intrínseca entre a lógica do descobrimento e a lógica da justificação é o aspecto mais importante do método de incorporação do lema.
Beta: E naturalmente compreendo agora suas enigmáticas observações anteriores sobre não se perturbar por uma conjectura ser ao mesmo tempo comprovada e refutada e sobre sua disposição de comprovar inclusive uma falsa conjectura (LAKATOS, 1978, p. 56).
Pode-se complementar essas colocações com a observação de um dos alunos, Sigma: “Assim, não apenas as refutações atuam como fermentos para a análise da prova, como estas podem agir como agente fermentador para refutações” (LAKATOS, 1978, p. 70).
Esses aspectos reforçam a ideia de que os questionamentos gerados ao longo do processo fazem surgir alguns contraexemplos que podem ser interpretados como monstros. Quando isso ocorre, significa que surgiram exemplos de poliedros que não atendem as definições e teoremas estabelecidos de acordo com a visão eureliana. Na visão de Cardoso (1997), Lakatos descreve que esses monstros podem ser apresentados das seguintes formas:
- locais, mas não globais, os quais podem refutar os lemas gerados nas discussões, mas não a conjectura principal. Nestes casos, há aperfeiçoamento dos lemas desenvolvidos e de suas provas, que podem ser reelaboradas e substituídas;
- locais e globais, que como não estão de acordo nem com a conjectura principal nem com os lemas e, portanto, não refutam nada;
- globais, mas não locais, os quais refutam a conjectura principal e ajudam a encontrar os lemas ocultos.
Segundo a autora, inicialmente, Lakatos usa contraexemplos globais para promover as críticas da conjectura e da análise da prova. A partir deles o conceito de poliedro é redefinido várias vezes.
São esses aspectos que geram os processos de provas e refutações. Segundo Cardoso (20017, p. 44), “o conhecimento matemático só avança quando admitimos refutações heurísticas ou lógicas. As heurísticas estimulam novos experimentos fazendo o conteúdo crescer”.
Os apêndices de Provas e Refutações, também exploram as ideias mencionadas sobre o método de provas e refutações e o enfoque heurístico.
O primeiro apêndice diz respeito à história da convergência uniforme do Cálculo Diferencial. Nessa construção, o autor também mostra a dinâmica de Provas e Refutações e inclui diálogos entre alguns personagens como Cauchy, Abel, Fourier e Seidel, por exemplo. São observadas críticas em relação à metodologia euclidiana, a qual é considerada como um obstáculo ao desenvolvimento das teorias Matemáticas.
Fatos históricos relevantes à tese de Lakatos são desenvolvidos ao longo desse apêndice. Cardoso (1997) descreve que o autor estrutura as seguintes etapas:
É apresentada uma conjectura ingênua de Cauchy, a qual trata do limite de séries convergentes de funções contínuas.
Uma prova ingênua é oferecida por Cauchy. A partir do Princípio de Continuidade de Leibniz, esse personagem explora o axioma da continuidade e, interpreta que a prova, no caso considerado, é algo trivial.
Séries trigonométricas de Fourier são então utilizadas como refutações.
As análises da prova passam a surgir. Buscam-se formas diferentes para salvar a conjectura, por meio da descoberta do lema oculto, proposto por Seidel, e do método anti-exceção, abordado por Abel.
Surge o conceito de convergência uniforme, representando, assim, a conjectura aperfeiçoada.
No caso do segundo apêndice são tratadas considerações a respeito das vantagens em se adotar o método heurístico de Provas e Refutações. Nesse momento são explorados três conceitos matemáticos: a convergência uniforme, a variação limitada e a definição caratheodoríca de sequência mensurável.
Lakatos destaca nessa seção sua oposição frente ao estilo dedutivista, imposto pela metodologia euclidiana. O autor descreve que “a lista de axiomas e definições é seguida de teoremas cuidadosamente redigidos [...] carregados de pesadas condições” (LAKATOS, 1978, p. 185). Essa afirmação é complementada com preocupações da postura de um estudante que esteja sujeito a essa abordagem. Neste caso, o indivíduo deve aceitar o ritual euclidiano sem questionamentos sobre o assunto ou sobre como o mesmo foi elaborado/praticado. E, ainda:
no estilo dedutivista, todas as proposições são verdadeiras e válidas todas as inferências. A Matemática é apresentada como uma série sempre crescente de verdades imutáveis e eternas. Possivelmente, não têm lugar contraexemplos, refutações e crítica. Um aspecto autoritário é garantido para o assunto, começando com definições antimonstro disfarçadas e geradas pela prova e com o teorema todo emplumado, suprimindo a conjectura primitiva, as refutações e a crítica da prova. O estilo dedutivista esconde a luta, esconde a aventura [...] o resultado final é exaltado como infabilidade sagrada (LAKATOS, 1978, p.186).
Segundo Lakatos, o estilo heurístico dá ênfase à situação problema, pois ela abrange a lógica que dá origem ao nascimento do novo conceito. Ao fim do apêndice, o autor afirma que outros exemplos poderiam ser detalhados seguindo o processo heurístico, dissipando o misticismo autoritário que envolve a Matemática abstrata. Seria possível atuar, então, com a degeneração, que segundo Lakatos (1978), faria muito bem à Matemática. No entanto, o estilo dedutivista e a atomização do conhecimento matemático ainda perduram nessa área de estudos.
Por isso, a proposta deste trabalho é contribuir com possibilidades de se realizar uma abordagem de problemas matemáticos, que tenham perspectivas semelhantes ao que foi explorado por Lakatos, utilizando princípios heurísticos (os quais também foram trabalhados por George Polya e serviram de inspiração para as Filosofias lakatosianas).
A seguir, será apresentada uma caracterização geral de um problema nos moldes do PBL, visando atender alguns princípios que aqui foram apontados. Posteriormente, são explanadas possíveis relações entre a estruturação de um problema nesse formato e uma sugestão de como o mesmo poderia ser contemplado mediante as explanações realizadas.
Delineando a exploração de um problema na perspectiva do PBL
Neste estudo foram indicadas algumas perspectivas lakatosianas e a intenção é propor que a resolução de um problema matemático seja desenvolvida mediante tais reflexões. Todavia, intenciona-se explorar esses princípios, considerando a ideia de que a Matemática é uma ciência que está diretamente atrelada a outras áreas de conhecimento. Ou seja, propõe-se algumas proximidades entre enfoques encontrados na obra Prova e Refutações e a estruturação de um ambiente de ensino que estimule a aprendizagem. Pretende-se valorizar tanto o conhecimento matemático, como a sua não imparcialidade em outras áreas, considerando aspectos humanos e sociais.
Desse modo, essas conexões podem ser viabilizadas por meio da resolução de um problema amparado na visão do PBL. Conforme Ribeiro (2008), os contornos de um problema nessa perspectiva são dados tanto pelas especificações que nele estão contidas como também pelas limitações do contexto no qual está inserido. Para o autor, esse problema pode ser um desafio acadêmico, no qual é possível realizar um recorte do conteúdo disciplinar, ou um cenário, real ou realístico, relacionado com alguma prática profissional, social, dentre outras associações. Neste sentido, um problema no PBL pode permitir que a dualidade teoria e prática seja explorada, ou seja, pode-se relacionar o conhecimento e o fazer matemático (amparados em princípios lakatosianos) e, também explorar outros campos de conhecimento que, no caso, estão ligados a possíveis aspectos de nossa sociedade.
Barrows e Tamblyn (1980), que foram os percursores do trabalho com o PBL, relatam que o uso de problemas pode estimular a aplicação de habilidades de resolução de problemas ou de raciocínio e destacam que o mesmo não é oferecido como um exemplo da relevância da aprendizagem anterior, nem um exercício de aplicação. O problema é apresentado antes da explanação do conteúdo e o levantamento de hipóteses, geradas por discussões entre os pares envolvidos, permitem que os conhecimentos sejam desenvolvidos (elaborados, refutados, demonstrados).
Sendo assim na próxima seção são estabelecidas algumas possíveis aproximações entre a abordagem de um problema no PBL e reflexões embasadas nas ideias de Lakatos.
Estabelecendo algumas relações
A perspectiva deste estudo procura mobilizar a abordagem de problemas matemáticos estruturados de acordo com o PBL, visando desenvolver uma característica quase-empírica, que sublinhe a relação entre Matemática e suas aplicações. Segundo Vithal, Christiansen e Skovsmose (1995) , este foi um aspecto da Filosofia da Matemática abordado por Lakatos.
Ainda nas palavras dos autores, Lakatos descreve uma Filosofia que está além da verdade Matemática, demonstrando que o processo histórico e o uso de experiências de pensamento, provas, refutações e diálogo, estão associados ao fazer matemático. Para eles,
Lakatos demonstrated formalism's lack of ability to describe the processes of creating and doing mathematics. In this way, Lakatos changed the question from 'Why is mathematics true?' to 'How does agreement on mathematics come about?' He shifted the focus from formal to informal mathematics, from product to process (VITHAL; CHRISTIENSEN; SKOVSMOSE, 1995, p.217).
Embasando-se nesses ideais, esse processo associado ao fazer matemático pode estar inerente à resolução de um problema, perpassando interesses apenas nos resultados obtidos ou nas demonstrações realizadas. Um ambiente de estudos que propicie um processo de provas e refutações, como o descrito por Lakatos, no sentido de analisar conjecturas, investigar aspectos que giram em torno de sua prova, realizar descobertas, abordar conhecimentos intrínsecos à própria Matemática, pode ser contemplado por meio de um enfoque construtivo como o PBL.
Molina (1994) afirma que as provas (e derivações) em um sistema formal satisfazem uma série de exigências bem rígidas, mas que a Matemática informal demonstra flexibilizar essas exigências, dando mais liberdade ao desenvolvimento de todo processo que deve ser realizado. Busca-se explorar o conhecimento matemático de diferentes formas. Assim como ocorre em Provas e Refutações, em que a prova é contestada em vários momentos pelos alunos levando-os a propor outras reformulações e discussões, o conhecimento matemático passa a crescer, em comparação à uma estrategia apenas dedutiva. Propõe-se que relações análogas a esse processo possam ser fomentadas pela perspectiva de problemas que aqui é considerada.
Cardoso apresenta a conjectura dos poliedros desenvolvida por Lakatos do seguinte modo:
Apresenta-se uma conjectura ingênua;
Apresenta-se uma prova ingênua;
Surgem contraexemplos (refutações);
Faz-se uma análise crítica da prova a fim de corrigir os defeitos e reformular a conjectura inicial;
São examinadas outras provas e outros teoremas para verificar se há alguma ligação desses com a prova em questão;
Confere-se as consequências da conjectura original;
Abrem-se novos campos de investigação pela ligação do problema original com outros problemas. (CARDOSO, 1997, p.13).
A autora ainda destaca que os itens (5) ao (7) exploram a aplicação do conhecimento em si obtido por (1) a (4) em outros possíveis campos da Matemática, ou mesmo de outra ciência, estabelecida anteriormente.
Nesse sentido observam-se aproximações com a abordagem de um problema no formato do PBL, como proposto por Ribeiro (2008):
Apresenta-se um problema aos interessados, os quais organizam suas ideias embasando-se nos conhecimentos prévios que possuem a respeito do assunto.
Diálogos e discussões iniciais fazem surgir as chamadas questões de aprendizagem.
Essas questões levantadas permitem que os envolvidos decidam quais delas serão investigadas (bem como os recursos que possuem para tal) e definem qual o papel de cada participante na investigação que deverá ser realizada.
Há reencontros dos participantes em outros momentos. As questões levantadas anteriormente são integradas aos seus novos conhecimentos, que foram sendo construídos no decorrer do processo de investigação do problema. Ocorre o compartilhamento das pesquisas e das possíveis conexões entre o problema e o que investigaram. Novas questões de aprendizagem são definidas à medida que há progressos na solução do problema.
Após a conclusão do trabalho com o problema, os participantes avaliam a viabilidade da solução encontrada, bem como realizam uma avaliação de si mesmos e de seus pares.
Com essas explanações, pode-se pensar em possíveis aproximações:
- o trabalho com um problema e a abordagem descrita por Lakatos, ocorre a apresentação de assuntos de interesses que mobilizam discussões e propiciam novas aprendizagens;
- a partir da problematização dada, em Provas e Refutações, emergem contraexemplos, e na abordagem do problema com o PBL, surgem as questões de aprendizagem, que podem englobar exemplos similares ao que foi dado como também de contraexemplos para as propostas elencadas.
- o processo da conjectura de poliedros, observado na descrição de Lakatos, suscitou o levantamento de diversas questões e possibilidades de soluções para a situação apresentada pelo professor. No trabalho com o problema PBL isso pode ocorrer de modo semelhante, no sentido de levantar hipóteses, de ter abertura para que novas possibilidades de resolução sejam discutidas, bem como corrigir defeitos e reformular as ideias, demonstrações já obtidas - possibilitando diálogos construtivos, refutações e análises das “verdades” observadas até ali.
- o processo de críticas sobre o assunto abordado, pode ser verificado em ambas as situações;
- tanto na sala de aula imaginária de Lakatos, quanto em uma abordagem com o problema PBL, os novos conhecimentos são reexaminados e têm suas compreensões retornando sempre a situação apresentada originalmente.
- e, conforme Cardoso (1997), novos campos de investigação gerados a partir da relação entre o problema original e outros problemas, são abertos.
- em ambos os casos, pode-se fomentar a valorização do saber matemático, destacadas não apenas pela abordagem de sistemas formais e demonstrações, mas amparadas em processos heurísticos, sujeitos a investigações e reformulações, que propiciem também a contemplação de aspectos históricos a respeito do conhecimento a ser desenvolvido.
A intenção deste estudo não é propor adaptações de um problema no formato do PBL como uma prescrição a ser seguida, a fim de explorar a Filosofia de Lakatos como um todo. As leituras realizadas a respeito desse autor podem gerar novas reflexões a alguns ideais que já vem sendo trabalhados acerca da abordagem da Matemática formal e de olhares que possibilitem outras descobertas.
Procurou-se pontuar certas proximidades entre a obra Provas e Refutações e a resolução de um problema construído na perspectiva do PBL. Existem distanciamentos entre ambos, como o fato de que o processo descrito por Lakatos, visa o enfoque do conhecimento matemático em si, enquanto um problema PBL, procura englobar enfoques mais interdisciplinares, estabelecendo relações entre conhecimentos teóricos e práticos, que não se limitam a determinada especificidade. Outro diferencial que se pode descrever é que Lakatos explora a Filosofia da Matemática, sem ter preocupações efetivas a respeito da Educação Matemática. No caso, de uma abordagem com o PBL, de modo geral, pode-se explorar tanto a Filosofia da Matemática quanto a Filosofia da Educação Matemática.
As perspectivas aqui mencionadas vislumbravam, em consonância com Lakatos, amparar-se em estrategias que não foquem apenas na busca por certezas Matemáticas e na contemplação de aspectos formalistas. Assim como Vithal, Christensen e Skovsmose (1995) descrevem, os participantes de sua pesquisa descobriram que também estavam experimentando a unidade de provas e refutações em seu processo de trabalho com projetos amparados em problemas, estas reflexões também se amparam em tais relações. Sendo assim, os princípios fundamentais, retratados na obra analisada, se aproximam do uso e desenvolvimento de problemas desenvolvidos de acordo com o PBL, contribuindo assim com o entendimento de como os processos acerca do conhecimento envolvido se estabelecem no campo filosófico, sejam eles matemáticos ou não.
Considerações finais
Neste estudo foram apresentadas considerações a respeito de princípios filosóficos destacados por Lakatos, em sua obra Provas e Refutações e, possíveis relações com a abordagem de problemas matemáticos. Procurou-se mencionar nas primeiras seções aspectos inerentes às ideias lakatosianas, contemplando alguns apontamentos que poderiam ser associados ao trabalho com problemas.
Uma breve caracterização de um trabalho com problemas explorados segundo a visão do Problem-Based Learning foi explanada, descrevendo as motivações e proximidades que levaram à construção destas reflexões. Posteriormente, partiu-se para algumas aproximações em si, destacando-se, inclusive, aspectos que Vithal, Christensen e Skovsmose (1995) realizaram em suas observações.
A intenção deste estudo não é afirmar que qualquer problema matemático possa explorar processos filosóficos descritos por Lakatos. No entanto, alguns encaminhamentos de trabalho podem ser delineados sob esses princípios.
Um problema em Matemática pode ser pensado como um modo de relacionar tanto o campo matemático quanto outras áreas de conhecimento, considerando que o falibilismo, o racionalismo de Lakatos e contextos relacionados à nossa realidade. Isso possibilita que as aplicações e reflexões geradas pelas análises e resolução do problema possam contribuir com a produção de novos conhecimentos. Embora existam diversas particularidades sobre a obra Provas e Refutações e a caracterização de um problema no PBL, algumas reflexões entre ambas foram construídas, a fim de contribuir com o crescimento dos conhecimentos contemplados e, mais ainda, com o crescimento de nossos estudantes.